Что такое пределы в математике: как их решать с примерами и образцам

Содержание

1. Как понять пределы в математике?
2. Виды неопределенностей в пределах
3. Как работает правило Лопиталя при решении пределов?
4. Заключение

Теория пределов в высшей математике относится к разделу анализа, который вместе с использованием таких моментов, как системы линейных уравнений доставляют многим студентам достаточно много хлопот. Особенно это касается тех, у кого имеются определенные проблемы с этим предметом. Для решения предела применяется ряд важных математических хитростей, в том числе проводить выбор по поиску определенного решения для выявления необходимого ответа на тот или иной пример.

В данной статье вы сможете понять пределы своих возможностей в этой области математической науки. Мы расскажем, каким образом вы сможете понять пределы в высшей математике.

Как понять пределы в математике?

Самое главное, что следует понять – что с собой представляет предел, а также предел чего имеется в виду? В некотором роде можно говорить о пределах числовых последовательностей, а также их функций. При этом в данном вопросе больше всего должно интересовать именно предел функции, именно они чаще всего попадаются множествам студентов.

Это важно!
Допустим то, что имеется некоторое переменная с определенной величиной. В случае, если величина во время изменения будет неограниченно приближаться к некоторому числу с, то тогда с и будет являться пределом величины. Для конкретного числа в определенном интервале функции f(x)=y пределом считается такое число С, которая будет стремиться функция при х, стремящаяся к точке с. Точка с будет принадлежать данном интервалу, на которой будет определяться та самая функция.

Хотя и звучит это достаточно страшно, но записывается такое достаточно просто. Она выглядит следующим образом:

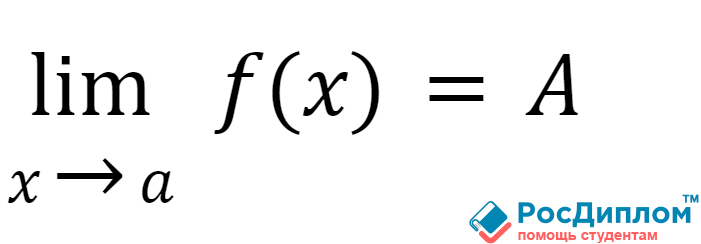
Функция Lim в вышепредставленной формуле происходит от английского слова limit, что переводится как предел.

Также имеется геометрическая сущность и объяснения данного определения, но мы не будет лезть в теоретическую часть, так как лучше всего запоминается информация на практике. В тот момент, когда мы начинаем утверждать, что х стремится к определенному значению, то нужно принять определенное число, которое будет бесконечно близко приближаться к нему.

В качестве конкретного примера приведем одну задачу, в которой следует найти предел.

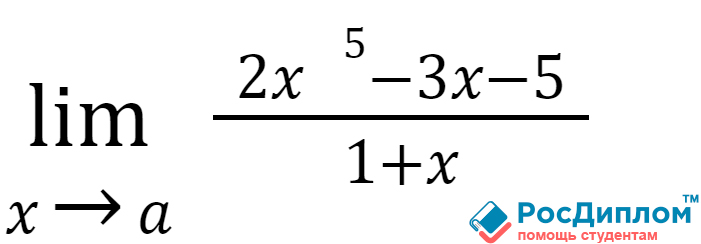
Для решения подобной задачи в качестве значения используем x=3 в функцию. Тогда получим следующее решение:

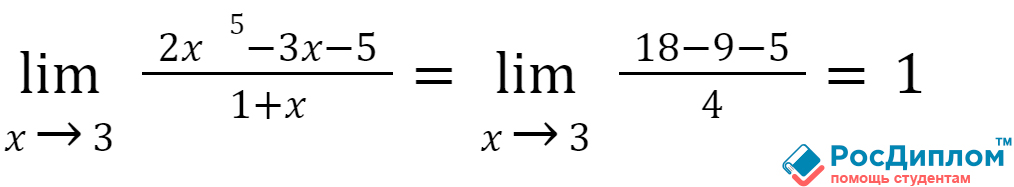
В примерах число х может стремиться к совершенно любому значению, в качестве которого можно выбрать совершенно любое число до бесконечности. Если мы подставим бесконечность, то тогда получим следующий ответ:

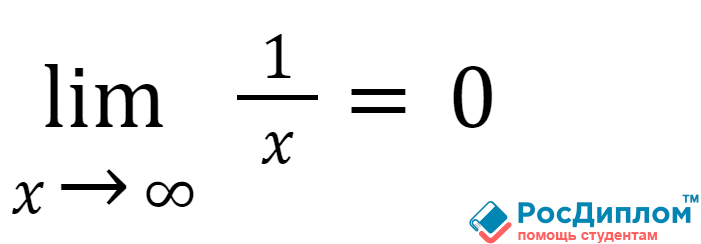
Как вы можете понять, чем больше будет использовано число в знаменателе, тем меньшим будет приниматься сама функция..

Как мы можем видеть на рассматриваемом нами примере, для решения предела следует просто подставлять в имеющуюся функцию то значение, к которой будет стремиться сам х. При этом он считается достаточно простым случаем. В реальности же процедура по нахождению предела не является настолько очевидной. В различных пределах могут встречаться неопределенности, имеющие вид 0/0 или бесконечность/бесконечность. В таких случаях многие прибегают к определенным хитростям, которые могут упростить задачу при решении.

Виды неопределенностей в пределах

Бывает достаточно большое количество различных типов неопределенностей, которые будут рассмотрены ниже.

Неопределенности вида бесконечность/бесконечность

Например, пусть предел будет иметь следующую формулу:

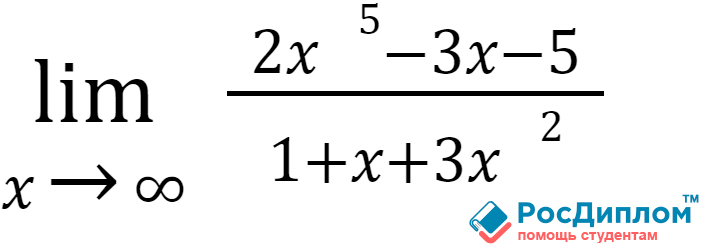
В случае, если мы будет пробовать в данную функцию подставлять бесконечность, то в итоге результатом будет бесконечность в обеих частях: числителе и знаменателе. В целом, необходимо говорить о том, что при решении такого рода неопределенностей существует определённый момент искусства: следует заметить то, каким образом может быть преобразована функция, чтобы неопределенность можно было искоренить. В данном случае следует разделить числитель, а также знаменатель на х, который будет в высокой от числа степени. Что в итоге у нас получится?

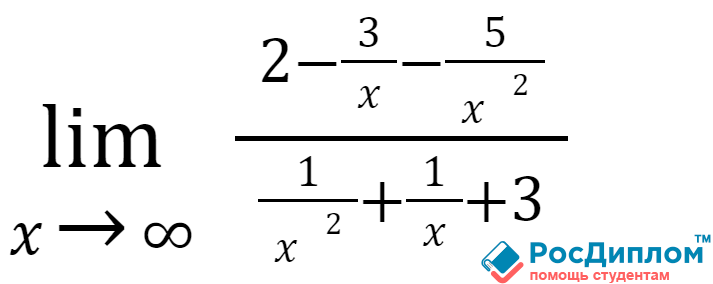
При изучении рассмотренного выше примера мы можем знать то, что все члены, которые будут содержаться в знаменателе х стремятся к нулевому значению, решением предела станет такое выражение:

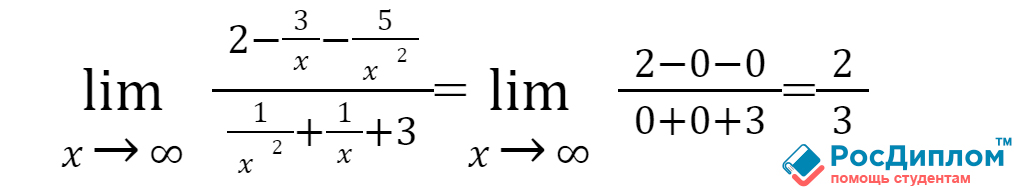
Чтобы раскрыть неопределенность подобного типа, следует делить числитель или знаменатель на большую от числа степень.

Другой вариант неопределенностей: 0/0

В данных случаях верным решением станет разложение числителей и знаменателей на множители. Но перед этим следует рассмотреть конкретный пример, чтобы понять всю суть действия. Вычислим следующий предел:

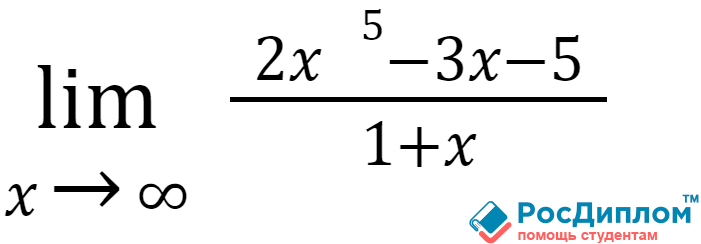
Как всегда, подстановка в нашу с вами функцию значения x=(-1) будет приводить нас к тому, что в обоех частях будет равно нулю. Посмотрите немного повнимательнее и вы сможете заметить то, что в числителе имеется квадратное уравнение. Найдя корни мы сможем найти и само решение.

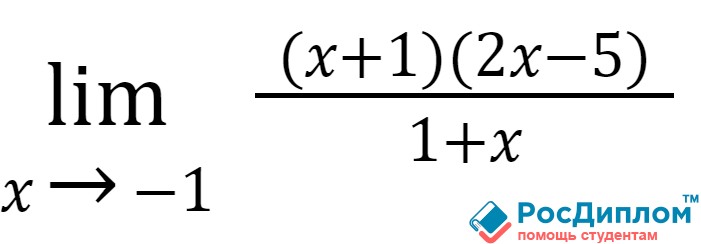
Во время сокращения мы сможем с вами получить следующее выражение:

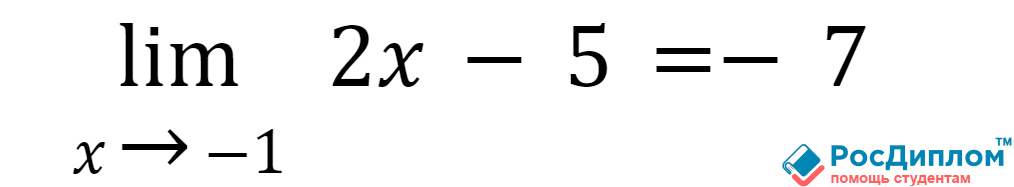
Если вы сталкиваетесь с неопределенностью, которая имеет тип 0/0, то вы можете смело раскладывать числитель и знаменатель на множители. Для упрощения процедуру по решению определенных примеров, мы решили привести следующую таблицу, в которой описаны пределы некоторых из известных функций:

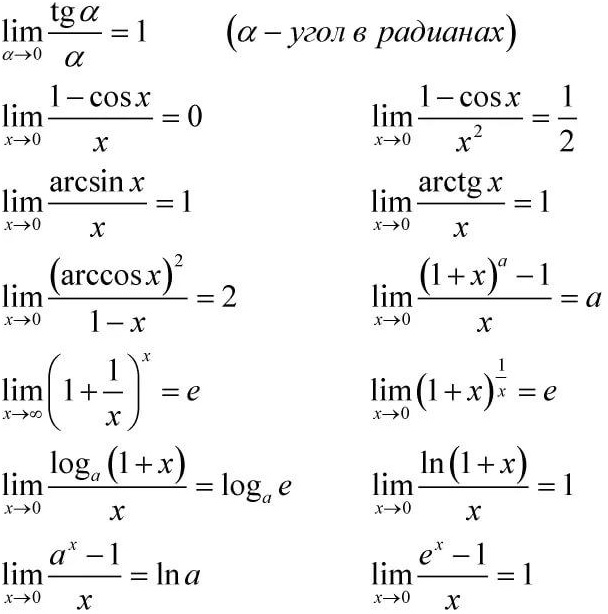
Как работает правило Лопиталя при решении пределов?

Если вам нужно изучить еще одну хитрость при решении неопределенностей обоих типов, то следует воспользоваться правилом Лопиталя. Но в чем же суть данного решения?

В том случае, если в пределе имеется неопределенность, то тогда будем брать производную от числителя и знаменателя до того момента, пока мы не решим её. Выглядит правило следующим образом:

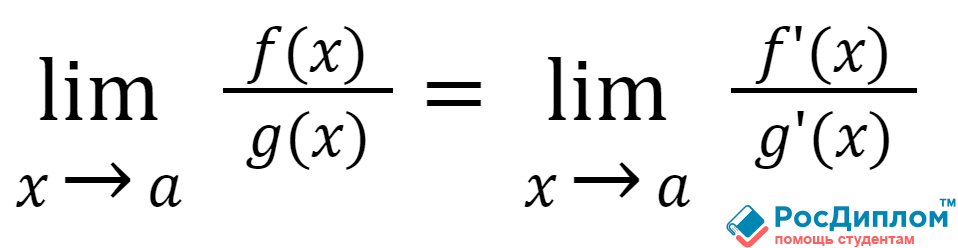
В наглядном примере вы сможете понять правило Лопиталя в действии:

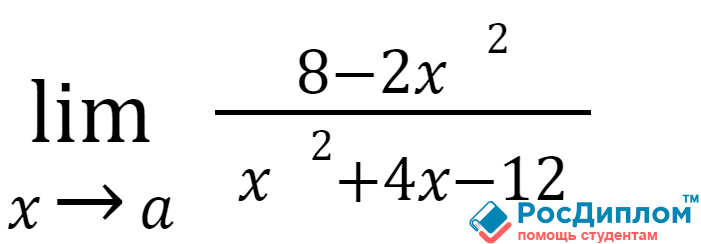
Тут мы можем понять, что нам попалась неопределенность типа 0/0. Теперь возьмем производные от числителя и знаменателя.

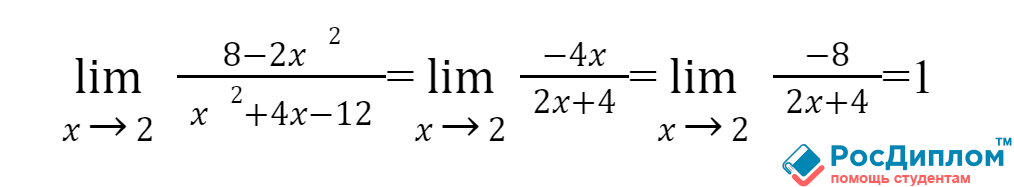
Таким образом, элегантно и достаточно быстро мы смогли устранить такой важный момент как неопределенность.

Заключение

Как вы можете понять, в нашем случае решение такого важного момента в высшей математики не является сложным. Главное приложить больше усилий при решении. Надеемся, что подобная информация, которая была описана в статье смогла помочь вам, и вы сможете использовать её при решении определенных функций. В основном решение сводится к некоторым хитростям и простой закономерности, которую следует учитывать.

На нашем сайте вы сможете найти любые другие статьи, которые будут полезны студентам, а также абитуриентам, планирующие поступать в те или иные ВУЗы. Кроме этого каждый пользователь сможет написать свой комментарий по поводу темы данной статьи. Возможно, у вас имеются определенные вопросы.

Компания «РосДиплом» на протяжении 20 лет занимается студенческими работами и предлагает помощь студентам во всех областях и темах. Наши преимущества: огромный опыт работы, лучшие авторы, собранные со всех уголков России, гарантии успешной сдачи и оптимальной цены, а также индивидуальный подход к каждому клиенту.