Как решать интегралы: примеры и образцы решения интегралов

Содержание

1. Что такое «интеграл»: разбираемся с понятием
   1. Неопределенный интеграл
   2. Определенный интеграл
2. Какие существуют правила вычисления интегралов?
   1. Свойства неопределенных интегралов
   2. Свойства определенных интегралов
3. Примеры решения интегралов
4. Заключение

Интегралы считаются одними из несложных заданий, который по сути дела можно понять, если правильно понимать саму математику. Если вы далеки от такой науки, то тогда эта статья точно для вас.

В ней вы сможете узнать: что это такое, даже если не знаете ничего об этих интересных функциях. Также вы узнаете, зачем нужен интеграл, каким образом он вычисляется, а также какие интегралы считаются определенными, а какие неопределенные.

Что такое «интеграл»: разбираемся с понятием

Такое слово, как интегрирование было зарождено еще в Древнем Египте. Разумеется, современного понятия там не было, но все же именно оттуда идут все истоки данных знаний. За многолетнюю историю человечества было написано несколько десяток книг по изучению данного вопроса.

В особенности отличится в вопросе изучения смогли такие личности научного мира, как Ньютон и Лейбниц. При этом суть понятий, о которых мы напишем ниже не изменилась. Единственное, что стало изменчивым, так это методы и способы решения.

Всего существует два типа интегралов – неопределенный и определенный. Ниже вы узнаете о том, чем они отличаются.

Неопределенный интеграл

Неопределенным называются те интегралы, которые имеют функцию F(y), производная равна функции f(y).

Другими словами интегралы являются обратной частью производной или же первообразная функция. На нашем сайте мы уже рассказывали вам о том, что такое производные, а также как их вычислять.

Существование первообразной будет распространяться для всех функций, которые считаются непрерывными.  Все первообразные будут совпадать по константе. Процедура по нахождению интеграла называется интегрирование.

В качестве простого примера может служить вот такая функция:

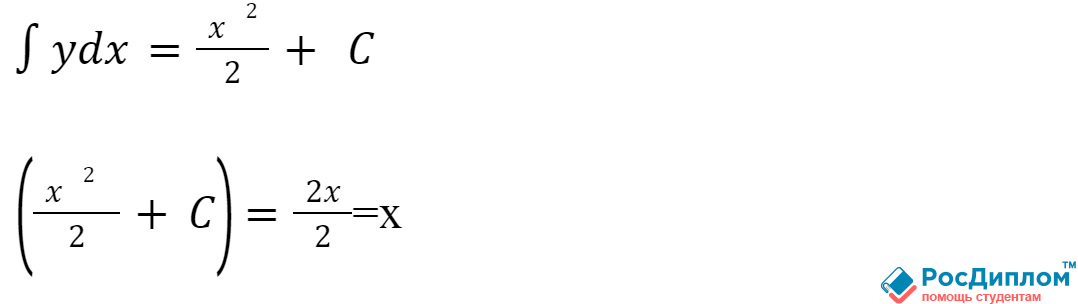
Чтобы упростить процедуру по вычислению первообразной различных элементарных функций, существуют таблицы, которыми вы сможете пользоваться для сокращения затрачиваемого времени при выполнении типовых заданий. Полная таблица первообразных выглядит следующим образом:

Определенный интеграл

В том случае, если вы никогда не имели дело с тем, что такое определенный интеграл вообще, то следует понимать о том, что человек работает с бесконечно малыми значениями. Интегралы позволяют вычислить площади простых или сложных фигур.

Необходимо понимать то, что интеграл – сумма огромного количества малых слагаемых. Чтобы понять это действие, представим для примера график любой функции, который показан на изображении ниже:

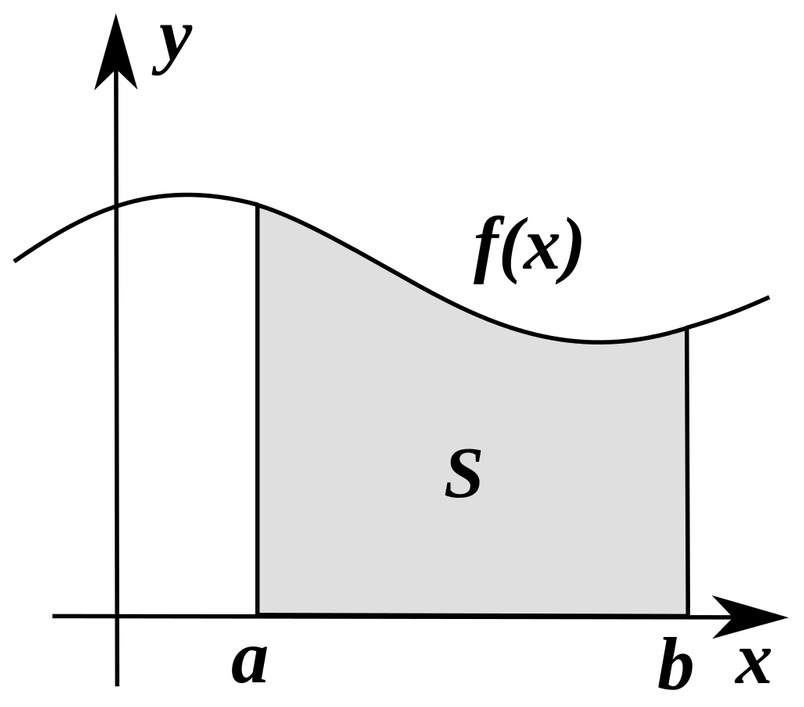
Каким образом находится площадь подобной фигуры, которая будет ограничиваться определенной плоскостью нашего графика? С помощью проведения расчетов интегрирования. Чтобы сделать это, необходимо разбить криволинейную трапецию, которая была ограничена осями координат, а также определенным графиком достаточно огромное количество мельчайших отрезков. Подобным образом фигура будет разделена на несколько тонких столбиков.

За сумму площадей столбиков следует считать площадь трапеции. При этом надо помнить то, что подобное вычисление не сможет дать точный результат. За точность результата отвечает такие понятия как узкие и маленькие отрезки. Чем они меньше и уже, тем точнее получится искомый результат. В том случае, если мы будем производить уменьшение их до данной степени, что вся её длина будет ближе всего к нулю, то само по себе сумма всех её площадей, которые различны отрезками будут стремиться к необходимой для нас при вычислении площади фигуры. Им собственно и будет определяться интеграл, который мы соответственно записываем вот в таком виде:

Какие существуют правила вычисления интегралов?

Ниже мы рассмотрим основные правила решения интегралов, которые поймут даже чайники, не понимающие в этом ничего.

Свойства неопределенных интегралов

Если вы не знаете, как решается неопределенный интеграл, то тогда ниже мы рассмотрим основные свойства, которые могут понадобиться во время решения любого примера.

• Производная от любого интеграла будет равняться подынтегральной функции:

• Константа выносится из-под волнистого знака интеграла:

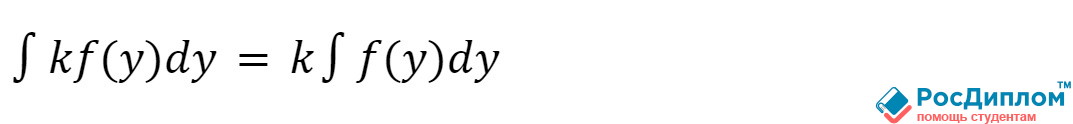
• Интеграл является зависимой от суммы всех полученных нами конкретных интегралов. Такое же свойство применяется при нахождении разницы интегралов:

Свойства определенных интегралов

К таким свойства определенных интегралов считаются следующие нижеописанные моменты (скрины к ним также будут подкреплены):

• Линейность функции:

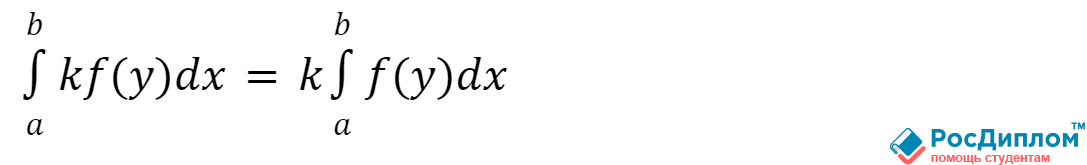
• Знак интеграла будет меняться – в основном происходит это в зависимости от того, каким образом будет происходить изменение различных пределов, которые связаны с интегрированием местами:

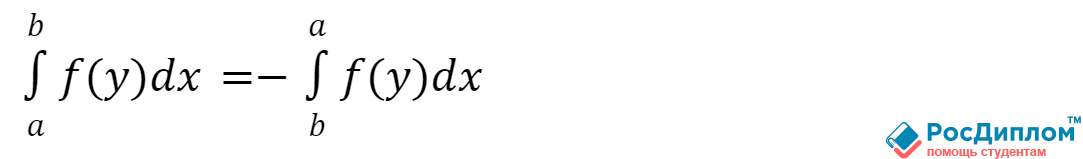
• Свойство при любых точках a, b и с:

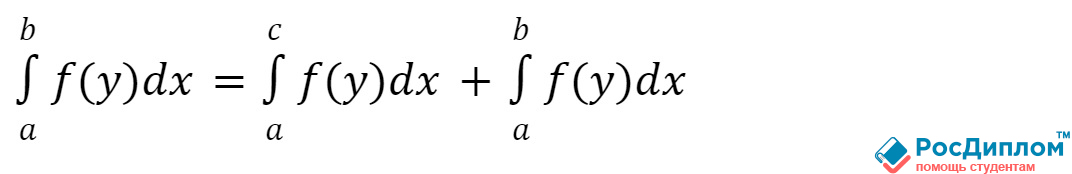
Каким образом происходит расчет интегралов? Все достаточно просто, необходимо лишь применить формулу, которая называется формула «Ньютона-Лейбница».

Как уже мы смогли выяснить выше, что определенный интервал считается пределом суммы. Но каким образом можно получить конкретное значение во время решения того или иного примера. Как уже было сказано выше, применяется так называемая формула «Ньютона-Лейбница», которая выглядит следующим образом:

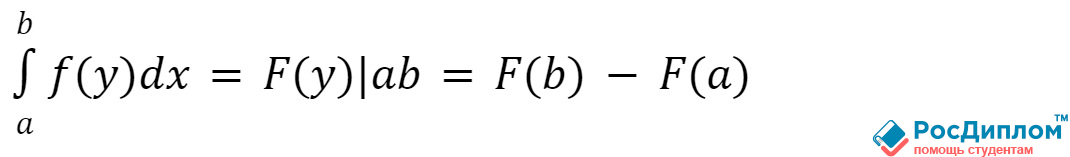
Примеры решения интегралов

Далее мы решили показать вам, каким образом будет проходить процедура по расчету интегралов с понятными примерами. Ниже описаны условия и решения данных заданий, которые могут быть. Всего мы решили показать вам 3 различных заданий, который отличается своей структурой и методикой решения.

Пример 1

Пример 2

Пример 3

Заключение

Надеемся, что в данной статье мы смогли рассказать вам об интегралах достаточно ёмко, чтобы вы начали в них разбираться. Если вы чего-то не понимаете, то можете написать в комментариях, где мы ответим на постоянные вопросы, связанные с интегрированием.

Компания «РосДиплом» на протяжении 20 лет занимается студенческими работами и предлагает помощь студентам во всех областях и темах. Наши преимущества: огромный опыт работы, лучшие авторы, собранные со всех уголков России, гарантии успешной сдачи и оптимальной цены, а также индивидуальный подход к каждому клиенту.