Решение производных: как решать производные с примерами и образцами?

Содержание

1. Какой геометрический и физический смысл имеют производные?
2. Какие существуют правила нахождения производной?
   1. Правило номер один: вынос константы
   2. Правило номер два: производная суммы функции
   3. Правило номер три: каким образом можно вычислить произведение производной функции
   4. Правило номер четыре: как вычисляется частное производной функции
3. Заключение

Решать любые задания с уклоном на физику или примеры по математике невозможно, если не иметь знания о том, что такое производная, а также какие методы вычисления существуют. В современной высшей математики производная считается важнейшей из ныне существующих понятий, которая применяется для анализа. Именно об этой фундаментальной теме мы и решили рассказать сегодня в нашей статье.

В данной статье каждый сможет узнать всю подробную информацию, связанной с геометрическим и другими смыслами данного момента, а также как происходит подсчет производной функции.

Какой геометрический и физический смысл имеют производные?

Представим то, что у нас имеется функция f(x), которая была задана в определенном интервале – они будут обозначены буквенными значениями a и b. Точки X и X0 принадлежат этому интервалу.

В момент изменения значения X изменяется и функция производной. Изменение аргумента является разностью его изначального значения X и X0. Полученная разность будет считаться дельта (обозначается небольшим квадратом) X и является приращением аргумента. Изменение или приращение функции с некоторых пор стали называть разностью значения функции, которые располагаются в двух удаленных друг от друга точках.

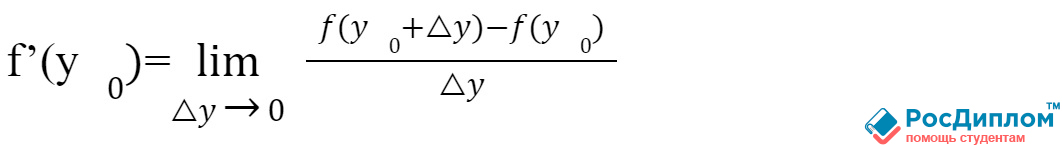
В другом смысле его можно записать в таком виде:

Многие задаются интересным вопросом – а какой имеется смысл в том, чтобы искать такой предел? А смысл есть, и он является основополагающим в этом вопросе.

В качестве геометрического смысла считается следующее утверждение: производная от функции будет равна точке тангенса угла, который находится между осью OX, а также привязанная к графику функции, связанной с конкретной точкой.

Физический смысл является следующим: производная пути по временному промежутку будет равен скорости для прямолинейного движения.

И ведь это действительно так – если вспомнить школьную программу, то каждому будет известно то, что скорость является частным пути x=f(t) и времени t. Чтобы рассчитать среднюю скорость за определенный промежуток пути, то следует воспользоваться следующей формулой:

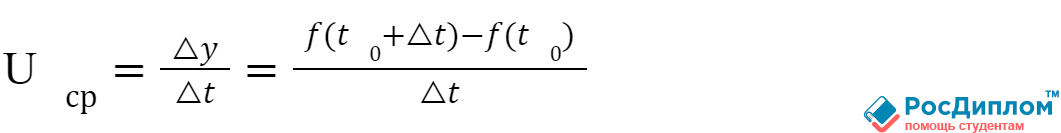
А для того, чтобы узнать скорость движения любого объекта в момент времени t0 (начального промежутка), то следует вычислить заданный предел:

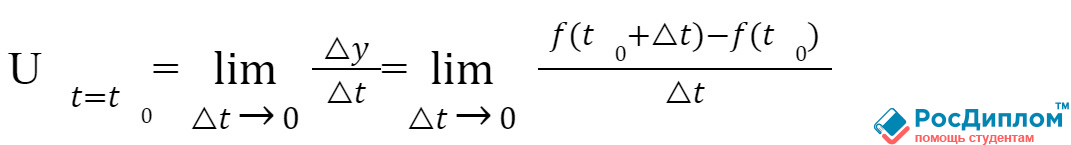
Ради того, чтобы вы смогли понять как это работает, приведем небольшой пример, позволяющий иллюстрировать применение производной. Пусть заданное нами тело будет двигаться по закону:

Нам необходимо рассчитать скорость в момент времени t=2 секунда. Таким образом нам нужно вычислить следующую производную:

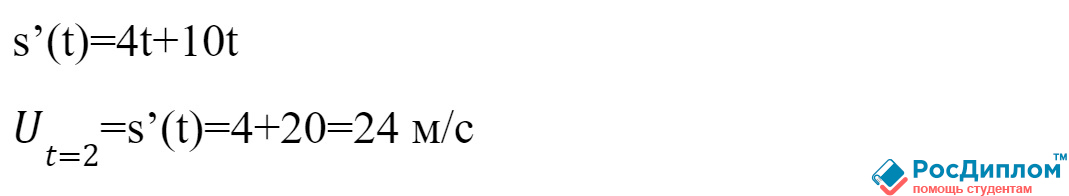
Какие существуют правила нахождения производной?

Сама процедура по нахождению производной имеет название дифференцирование. А так функция, которая будет иметь производную к определенной точке считается дифференцируемой. Так каким образом можно найти производную?

Если учитывать определение, то тогда необходимо будет составить отношение приращения всевозможных функций, в том числе вычислить определенный предел, который будет стремиться к нулю в момент приращения всего аргумента.

Разумеется, вычислять можно все имеющийся производные, но если говорить практической точки зрения, то это будет достаточно затяжным процессом. Все было разработано и показано до нас. Ниже имеется небольшая таблица, в которой имеются производные, имеющие элементарные функции. После этого мы будем с вами рассматривать определенные вычисления производных, в том числе те, которые имеют сложные функции с необходимыми примерами.

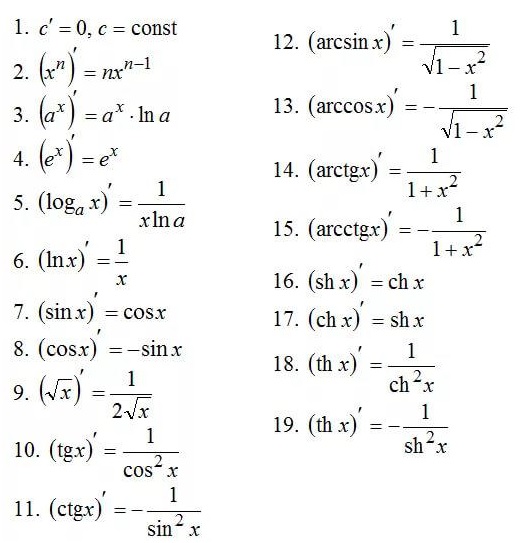
Правило номер один: вынос константы

Константу следует выносить за знак производной. Во время решения определенных заданий по математике в качестве основного правила вы можете просто выполнить упрощение выражения.

В качестве примера можно использовать следующую производную, которая вычисляется таким образом:

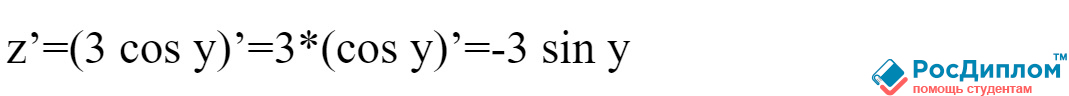
Правило номер два: производная суммы функции

Производная суммы двух различных функций будет равняться сумме производных этих функций. Также такое работает и для разницы производных в функции.

В качестве примера используется следующее выражение, где нужно найти производную:

Решением данного действия будет следующее:

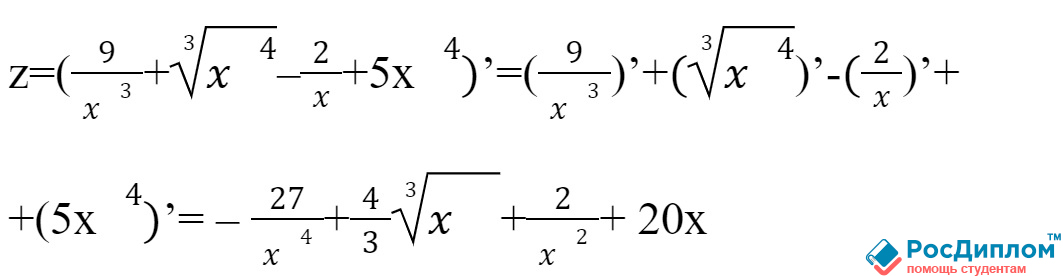
Правило номер три: каким образом можно вычислить произведение производной функции

В случае, если будет использоваться производная, в которой может быть произведение двух различных по виду функций нашего дифференцируемого выражения, то тогда её следует вычислять по следующей формуле:

В качестве примера возьмем следующее задание, где нужно найти производную функции:

В данном примере следует немного пояснить о вычислении производных, которые имеются у сложных функций. Производная для сложной функции будет равняться произведению определенной функции к её промежуточному аргументу на производную, связанную с промежуточным аргументом при использовании переменной, которая будет независимой.

В примере, который указан выше мы можем встретить вот такое выражение:

В этом случае нашим промежуточным аргументом считается 8х в 5-ой степени. Чтобы произвести вычисление подобного выражения, в самом начале следует считать производную внешней функции, которая будет соответствовать промежуточному аргументу. Затем вам следует умножить на производную, которая будет примыкать к самому промежуточному аргументу, работающей по переменной независимой в выражении.

Правило номер четыре: как вычисляется частное производной функции

Формула выглядит следующим образом:

Именно такие основополагающие правила будут применяться при решении производных. Обязательно запомните их, чтобы в будущем решать такие задания. Ниже мы разместим несколько заданий, с помощью которых вы сможете попробовать найти производную самостоятельно.

Заключение

В данной статье мы попытались рассказать всем, кто хочет знать, чем является производная на простейшем для обывателей языке, чтобы все смогли понять все основные моменты, в том числе смысл как в геометрическом, так и физическом смысле.

Стоит отметить то, что тема не является слишком простой, поэтому если вы хотите овладеть ею в совершенстве, то обязательно выполните те задания, которые мы оставили выше. С их помощью каждый сможет научиться решать подобные типы заданий.

Компания «РосДиплом» на протяжении 20 лет занимается студенческими работами и предлагает помощь студентам во всех областях и темах. Наши преимущества: огромный опыт работы, лучшие авторы, собранные со всех уголков России, гарантии успешной сдачи и оптимальной цены, а также индивидуальный подход к каждому клиенту.